Globally Consistent Normal Orientation for Point Clouds by Regularizing the Winding-Number Field
3The University of Texas at Dallas 4Qingdao University of Science and Technology
5Texas A&M University
Abstract
Estimating normals with globally consistent orientations for a raw point cloud has many downstream geometry processing applications. Despite tremendous efforts in the past decades, it remains challenging to deal with an unoriented point cloud with various imperfections, particularly in the presence of data sparsity coupled with nearby gaps or thin-walled structures. In this paper, we propose a smooth objective function to characterize the requirements of an acceptable winding-number field, which allows one to find the globally consistent normal orientations starting from a set of completely random normals. By taking the vertices of the Voronoi diagram of the point cloud as examination points, we consider the following three requirements: (1) the winding number is either 0 or 1, (2) the occurrences of 1 and the occurrences of 0 are balanced around the point cloud, and (3) the normals align with the outside Voronoi poles as much as possible. Extensive experimental results show that our method outperforms the existing approaches, especially in handling sparse and noisy point clouds, as well as shapes with complex geometry/topology.
Introduction
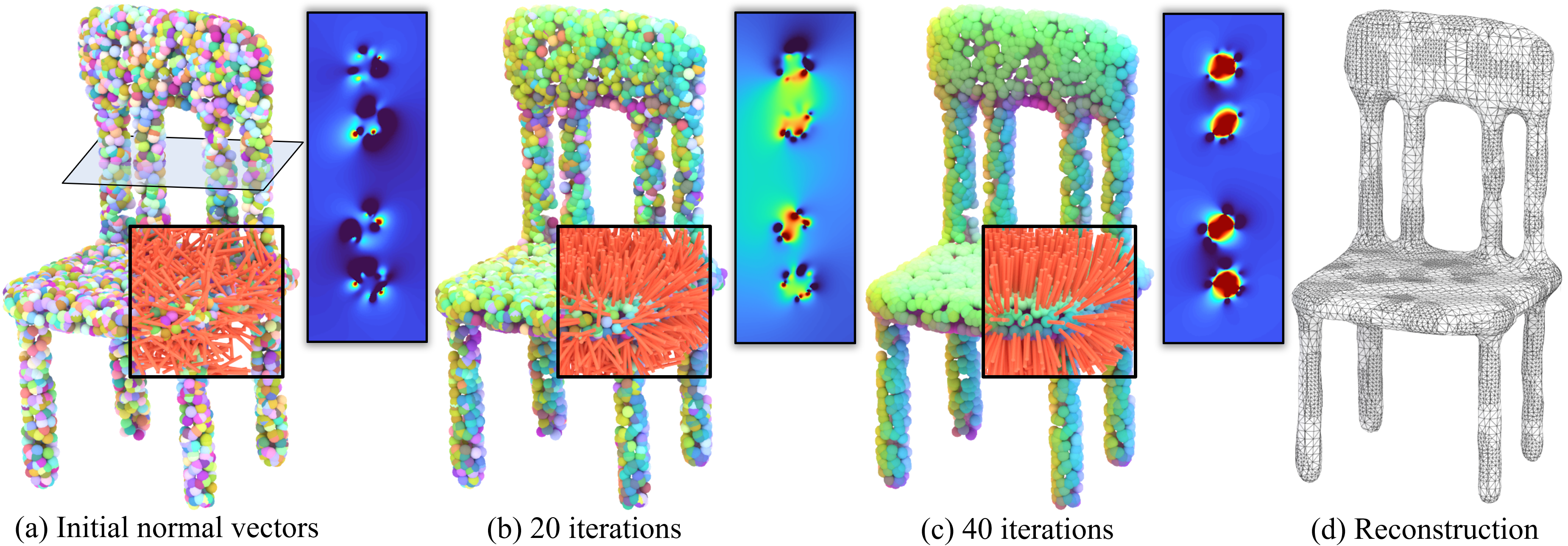
The optimization progress using our method. The input model is a thin board with randomly initialized normals (in orange) of the point cloud. We cut the board in the middle with a plane to show the sectional view of the winding-number field (visualized in a color-coded style)
In recent years, the winding number, as a powerful tool for inside outside tests, has gained increasing attention in digital geometry
processing, ranging from meshing to reconstruction. Despite the ability to
distinguish the interior part (the winding number is close to 1) from
the exterior part (the winding number is close to 0), it seriously
depends on the support of reliable normals. Our hypothesis is that
only when the normals are oriented with global consistency, the
winding-number field could be approximately binary-valued with
1 and 0. This inspires us to optimize the normals such that the
winding-number field becomes fully regularized.
In this paper, we propose an all-in-one functionality to characterize the
requirements of a winding-number field from three aspects: (a) the
winding number should be close to either 1 or 0 at any query point,
(b) when the query points are scattered in the neighborhood of input
samples p𝑖 , the occurrences of 1 and the occurrences of 0 should
be approximately balanced, and (c) the sample p𝑖’s normal vector
should align well with the direction towards the outside Voronoi
pole.
Results

We equip the input unoriented point clouds with our computed normals (rendered with RGB mapping). By feeding the points and the normals together into the screened Poisson reconstruction (SPR) solver, we get high-fidelity reconstruction results (in gray), which exhibit the high quality of the computed normals.
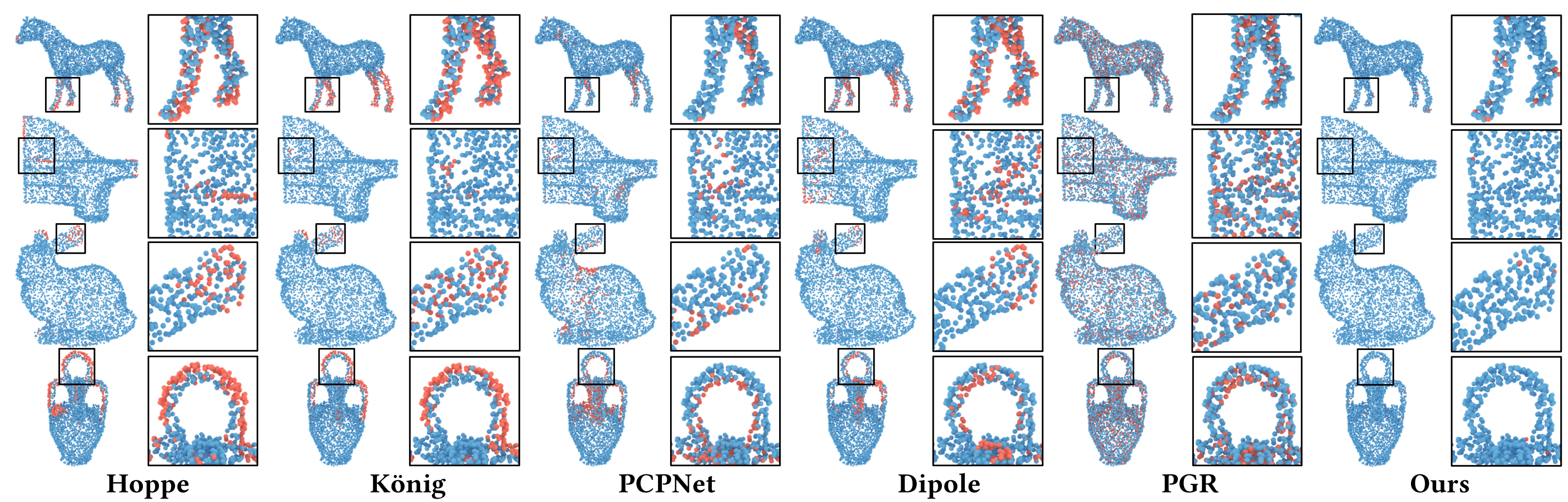
Comparison on the ratio of true normals between our approach and the existing five methods: Hoppe [Hoppe et al. 1992], König [König and Gumhold 2009], PCPNet [Guerrero et al. 2018], Dipole [Metzer et al. 2021] and PGR [Lin et al. 2022]. The true predictions and false predictions are colored in blue and red, respectively. Note that the level of Gaussian noise is 0.5%.
The Chair model contains thin-walled tubes and plates, as well as nearby gaps (see the highlighted region). Our approach can yield the highest truth percentage among the five approaches. Note that the false predictions are colored in red.
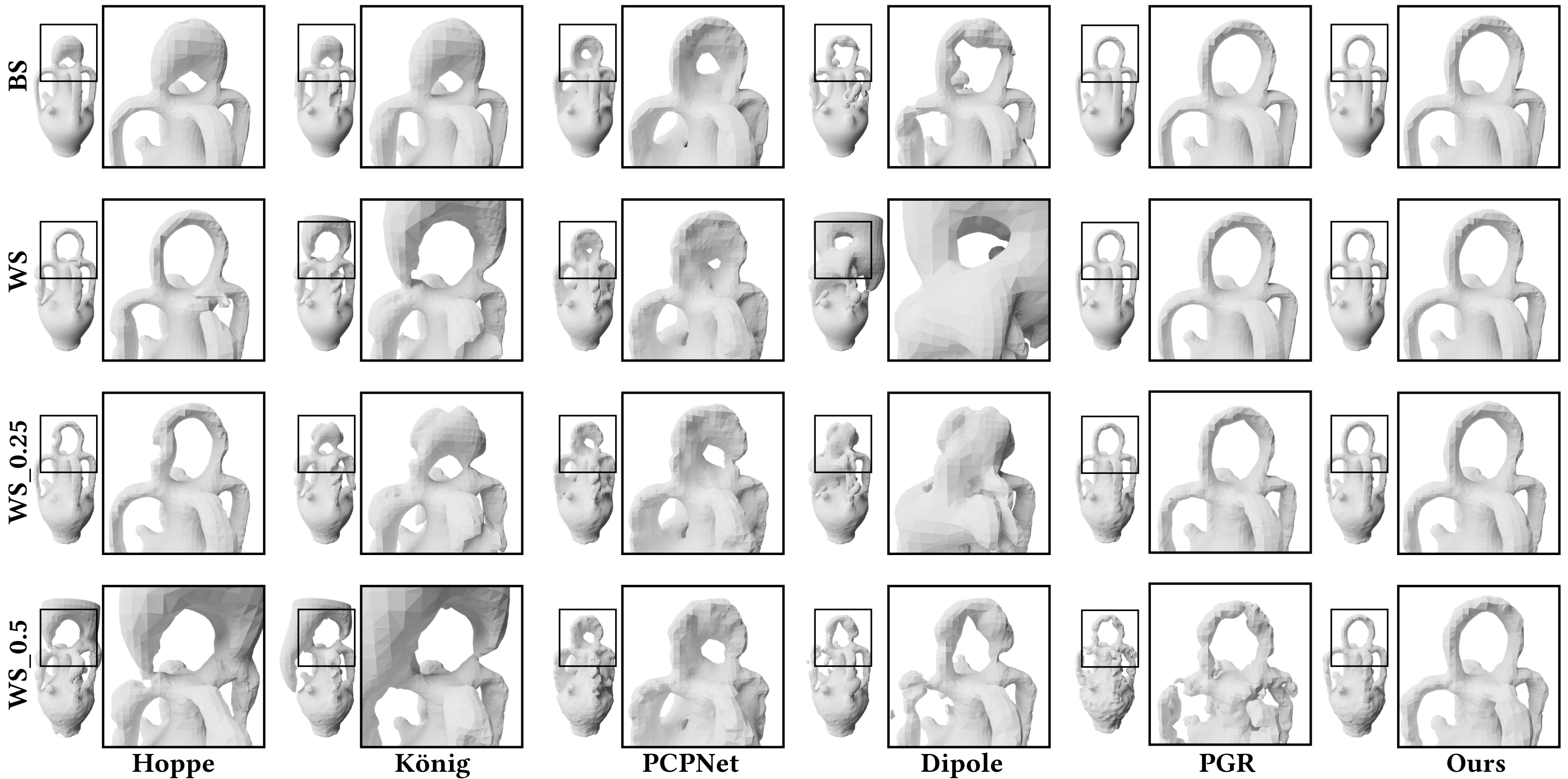
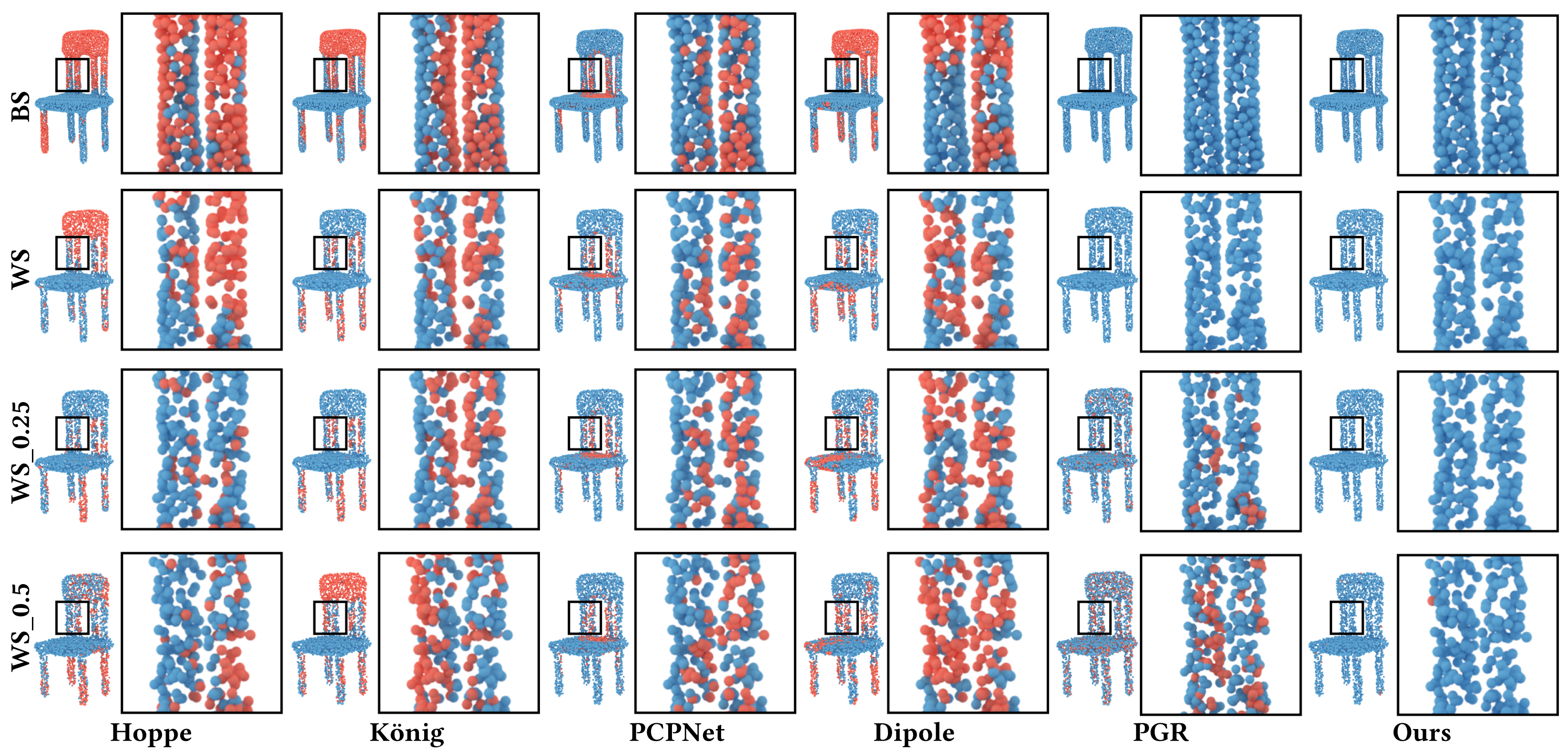
Visual comparison of the reconstructed surfaces at different sampling conditions and different levels of noise. We show results of four different sampling conditions: BS (blue noise sampling), WS (white noise sampling), WS_0.25 (white noise sampling with 0.25% noise) and WS_0.5 (white noise sampling with 0.5% noise).

Comparing the reconstruction quality on point clouds with 0.5% Gaussian noise.

Tests are made on sparse point clouds: 500 points, 750 points and 1K points. Our results are close to the ground truth for each of the three inputs. The comparison shows that our algorithm has a big advantage on sparse raw data.
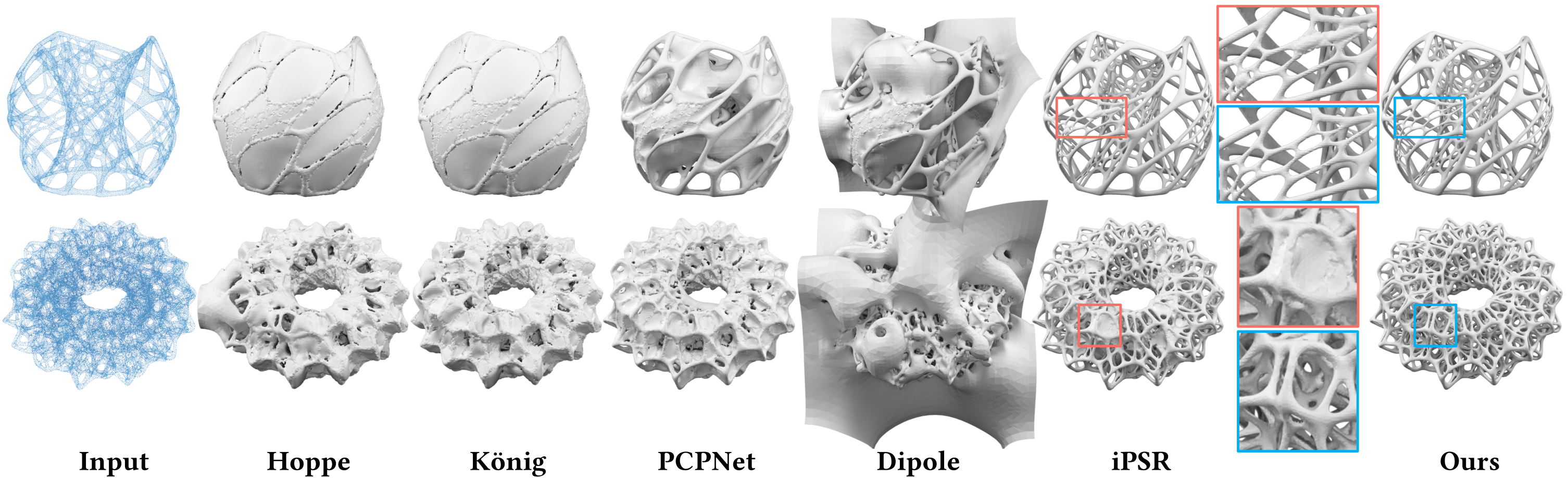
Tests on point clouds with highly complex topology/geometry. The model in the top row has 80K points while the model in the bottom row has 100K points.
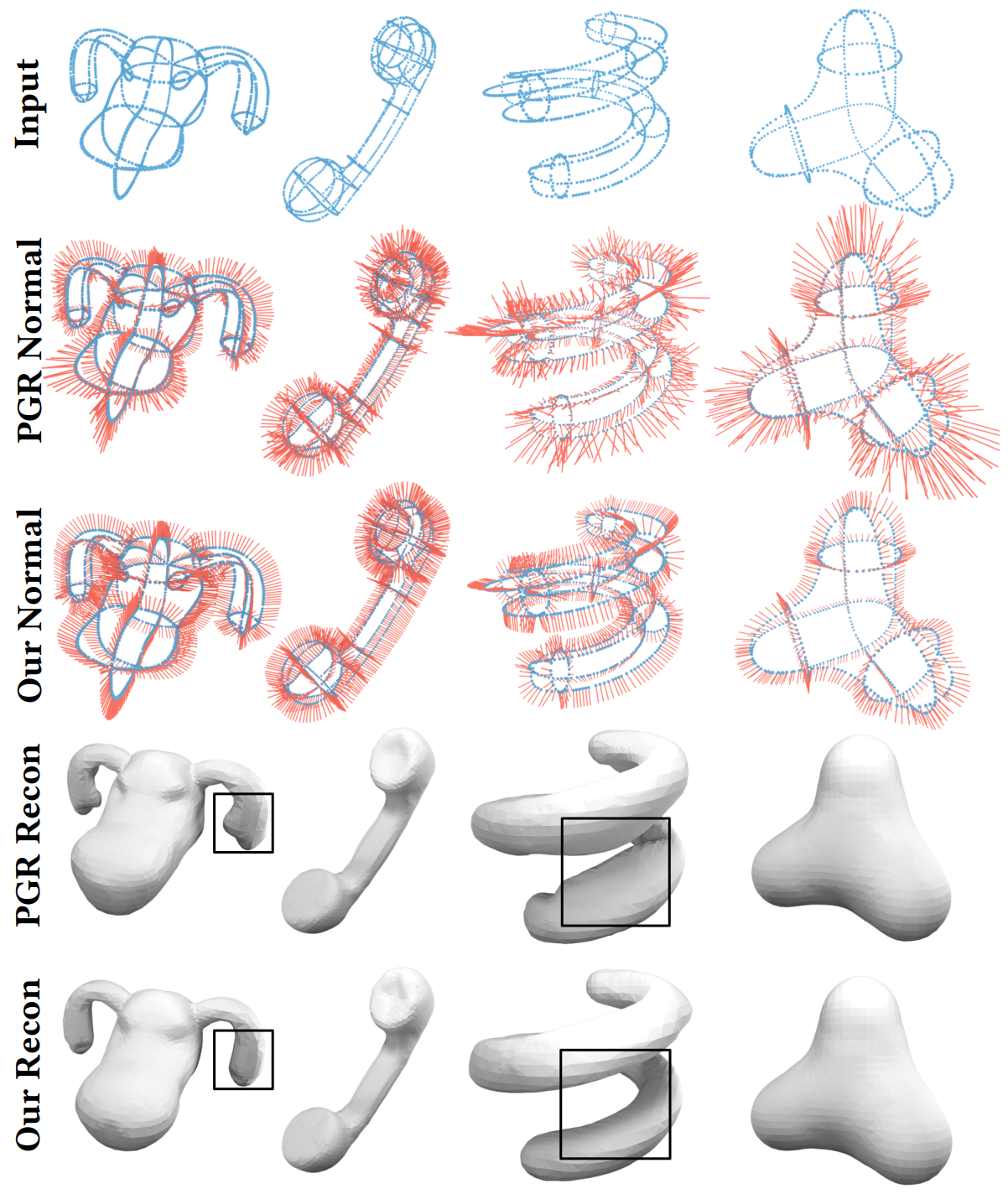
Normal estimation for wireframe-type point clouds. All the models are from VIPSS [Huang et al. 2019]. PGR may produce bulges around thin tubular structures.
Citation
@article{Rui2023GCNO,
author = {Xu, Rui and Dou, Zhiyang and Wang, Ningna and Xin, Shiqing and Chen, Shuangmin and Jiang, Mingyan and Guo, Xiaohu and Wang, Wenping and Tu, Changhe},
title = {Globally Consistent Normal Orientation for Point Clouds by Regularizing the Winding-Number Field},
year = {2023},
issue_date = {August 2023},
publisher = {Association for Computing Machinery},
address = {New York, NY, USA},
volume = {42},
number = {4},
issn = {0730-0301},
url = {https://doi.org/10.1145/3592129},
doi = {10.1145/3592129},
journal = {ACM Trans. Graph.},
month = {jul},
articleno = {111},
numpages = {15},
keywords = {normal orientation, winding number, Voronoi diagram, optimization, raw point cloud}
}Page last updated







